In my previous post I illustrated why it is not possible to compute the Jordan canonical form numerically (i.e. in floating point numbers). The simple reason: For every matrix 
with matrix 
where the matrix exponential is
It is not always simple to work out the matrix exponential by hand. The straightforward way would be to calculate all the powers of 
Its first powers are
You may notice that the Fibonicci numbers appear (and this is pretty clear on a second thought). So, finding a explicit form for 
Another way is diagonalization: If 
you see that
and the matrix exponential of a diagonal matrix is simply the exponential function applied to the diagonal entries.
But not all matrices are diagonalizable! The solution that is usually presented in the classroom is to use the Jordan canonical form instead and to compute the matrix exponential of Jordan blocks (using that you can split a Jordan block 
But in light of the fact that there are a diagonalizable matrices arbitrarily close to any matrix, on may ask: What about replacing a non-diagonalizable matrix
Let’s try this on a simple example:
We consider
which is not diagonalizable. The linear initial value problem
has the solution
and the matrix exponential is
So we get the solution
Let us take a close-by matrix which is diagonalizable. For some small
Since 
we get
The matrix exponential of 
Hence, the solution of 
How is this related to the solution of 
Of course, the lower right entry of 
is nothing else that the (negative) difference quotient for the derivative of the function 
and we get
as expected.
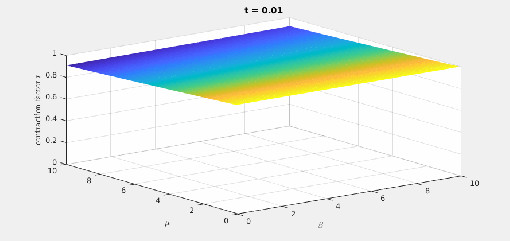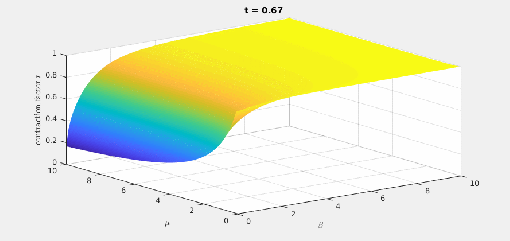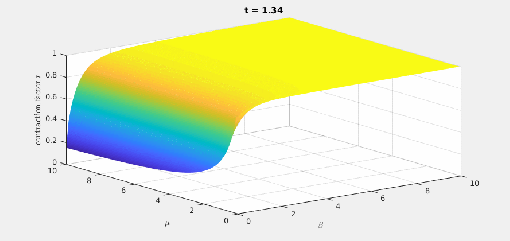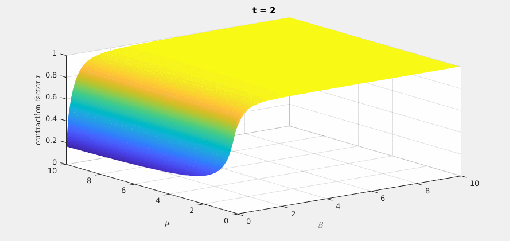
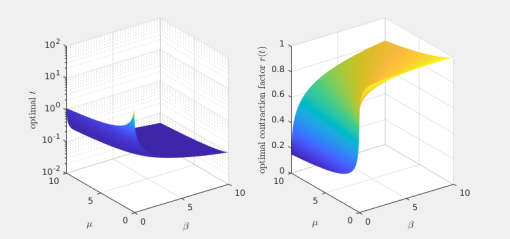
It turns out that a fairly big 
to $\e
. This matrix has 
as a double eigenvalue, but the corresponding eigenspace is one-dimensional and spanned by 
. To extend this vector to a basis we calculate a principle vector by solving
![{S = [v_{1}\, v_{2}]}](https://s0.wp.com/latex.php?latex=%7BS+%3D+%5Bv_%7B1%7D%5C%2C+v_%7B2%7D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002)
we get the Jordan canonical form of 
as
is not the Jordan canonical form of 
does not seem to be invertible and indeed we get
(which is my definition of diagonalizability). It does promise that 
and in fact
and we denote it by 
! (You probably have heard that before…) What does that mean numerically? Any matrix that you represent in floating point numbers is actually a representative of a whole bunch of matrices. Each entry is only known up to a certain precision. But this bunch of matrices does contain some matrix which is diagonalizable! This is exactly, what it means to be a dense set! So it is impossible to say if a matrix given in floating point numbers is actually diagonalizable or not. So, what matrix was diagonalized by MATLAB? Let us have closer look at the matrix 
:
is indeed just the inverse of the machine precision, so this inverse is actually 100% accurate. Recombining gives
.
where 
is the weight matrix, 
is the bias, 
is the input, and 
is the activation function. Usually 
) and the function mapping 
which applies 
and 
. So we need to take the derivative with respect to 
is a concatenation of the map 
and 
, the derivative of 
as linear maps in 
. So let’s rewrite the thing:![{W = [w_{1}\ \cdots\ w_{n}]}](https://s0.wp.com/latex.php?latex=%7BW+%3D+%5Bw_%7B1%7D%5C+%5Ccdots%5C+w_%7Bn%7D%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002)
and maps it by 
and 
is a matrix in 
, 
of compatible size we have that 
mapping 
can be rewritten as 
. Since 
is just a concatenation of 
) is calculated simply as 
(e.g. to produce a scalar loss that we can minimize), i.e. we consider the map 
![\displaystyle \begin{array}{rcl} \nabla F( \begin{pmatrix} \mathrm{Vec}(W)\\b \end{pmatrix}) &=& D\bar G( \begin{pmatrix} \mathrm{Vec}(W)\\b \end{pmatrix})^{T} DL(G(Wx+b))^{T}\\ &=& ([x^{T}\ 1]\otimes I_{m})^{T}\mathrm{diag}(\sigma'(Wx+b))\nabla L(G(Wx+b))\\ &=& \underbrace{( \begin{bmatrix} x\\ 1 \end{bmatrix} \otimes I_{m})}_{\in{\mathbb R}^{(mn+m)\times m}}\underbrace{\mathrm{diag}(\sigma'(Wx+b))}_{\in{\mathbb R}^{m\times m}}\underbrace{\nabla L(G(Wx+b))}_{\in{\mathbb R}^{m}}. \end{array}](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cbegin%7Barray%7D%7Brcl%7D++%5Cnabla+F%28+%5Cbegin%7Bpmatrix%7D+%5Cmathrm%7BVec%7D%28W%29%5C%5Cb+%5Cend%7Bpmatrix%7D%29+%26%3D%26+D%5Cbar+G%28+%5Cbegin%7Bpmatrix%7D+%5Cmathrm%7BVec%7D%28W%29%5C%5Cb+%5Cend%7Bpmatrix%7D%29%5E%7BT%7D+DL%28G%28Wx%2Bb%29%29%5E%7BT%7D%5C%5C+%26%3D%26+%28%5Bx%5E%7BT%7D%5C+1%5D%5Cotimes+I_%7Bm%7D%29%5E%7BT%7D%5Cmathrm%7Bdiag%7D%28%5Csigma%27%28Wx%2Bb%29%29%5Cnabla+L%28G%28Wx%2Bb%29%29%5C%5C+%26%3D%26+%5Cunderbrace%7B%28+%5Cbegin%7Bbmatrix%7D+x%5C%5C+1+%5Cend%7Bbmatrix%7D+%5Cotimes+I_%7Bm%7D%29%7D_%7B%5Cin%7B%5Cmathbb+R%7D%5E%7B%28mn%2Bm%29%5Ctimes+m%7D%7D%5Cunderbrace%7B%5Cmathrm%7Bdiag%7D%28%5Csigma%27%28Wx%2Bb%29%29%7D_%7B%5Cin%7B%5Cmathbb+R%7D%5E%7Bm%5Ctimes+m%7D%7D%5Cunderbrace%7B%5Cnabla+L%28G%28Wx%2Bb%29%29%7D_%7B%5Cin%7B%5Cmathbb+R%7D%5E%7Bm%7D%7D.+%5Cend%7Barray%7D+&bg=ffffff&fg=000000&s=0&c=20201002)
and hence, can be reshaped to a tupel 
matrix and an 
vector.
and 
, respectively, then 
represents the tensor product of the maps, 
. This relation to tensor products and tensors explains where the tensor in 
and 
, coming with two measures 
and 
. We also have a function 
which assigns a transport cost, i.e. 
is the cost that it takes to carry one unit of mass from point 
to 
. What we want is a plan that says where the mass in 
which says that thet mass in 
should be moved to 
. While natural, there is a serious problem with this: What if not all mass at 
as above. So, the map 
which map points in 
where 
stands for some set of functions on 
by 
. That’s good in principle, be we still run into problems when the target mass distribution 
on 
we look for a measure 
on 
as a transport plan.
it holds that 
).
of 
-cyclically monotone.
such that its 
.
is 
it holds that
and let 
be the usual scalar product. Then 
it holds that
somehow “moves up in 
, 
(
being the euclidean norm) seems more natural, right? But if we have a transport plan 
is 
, 
and all permutations 
it holds that
we get back the notion of 
is 
such that
is the 
and a permutation 
such that 
of 
and 
of 
such that for all 
and 
it holds that
: Take the mass of 
and shift it around. The full construction is a little messy to write down: Define a probability measure 
on the product 
as the product of the measures 
. Now let 
and 
be the projections of 
onto 
denotes the 
fulfills
. By definition of the 
by assumption, this gives
-Lipschitz + 
-strongly monotone, the iteration with stepsize 
converges linear with rate
there is a best 
and also a smallest contraction factor 
. Here are plots of these quantities:
from a Hilbert space into itself. Using the resolvent 
and the reflector 
, the Douglas-Rachford iteration is concisely written as
is monotone if 
, we can introduce a stepsize for the Douglas-Rachford iteration
and 
-strongly monotone, than the Douglas-Rachford iterates converge strongly to a solution with a linear rate
to get on optimal stepsize (in the sense that the guaranteed contraction factor is as small as possible). As Moursi and Vandenberghe explain in their Remark 5.4, this optimization involves finding the root of a polynomial of degree 5, so it is possible but cumbersome.
in the case of single valued 
in the domain (which has to be an interval) and then set
with 
.
is defined on a simply connected domain in 
we can recover 
from 
is convex if for every 
such that for all 
one has the subgradient inequality
as corresponding subgradient to 
is a (multivalued) monotone mapping. Recall that a multivalued map 
and 
it holds that 
. It is not hard to see that not every monotone map is actually a subgradient of a convex function (not even, if we go to “maximally monotone maps”, a notion that we sweep under the rug in this post). A simple counterexample is a (singlevalued) linear monotone map represented by
:
-cyclical monotonicity. In these terms we can say that a subgradient of a convex function is cyclical monotone, which means that it is 
. 
and set
. As a supremum of affine functions 
since 
everywhere). Finally, for 
we have
and this shows that 
. Now consider a path 
with 
. Then the term inside the supremum of~
. By monotonicity of 
, we increase this sum, if we add another point 
(e.g. 
, and hence, the supremum does converge to the integral, i.e.~
which satisfies 
and are increasing and convex (and thus, continuous). The definition of the Luxemburg norm in this case is
if 
.
are functions as 
if and only if 
. The proof that this construction indeed gives a norm is the same as in the one in the previous post.
-norms in different directions. Here is a simple example: In the case of 
we can split the variables into two groups, say the first 
variables. The first group shall be treated with a 
-norm. For the respective Luxemburg norm one has
functionals
.)
i.e., three-dimensional space, and picture the norm-balls (of level sets in the case the functionals 
and the first exponent to be 
and the second 
. The mixed norm is
:
and the same exponents. This makes the mixed norm equal to the 
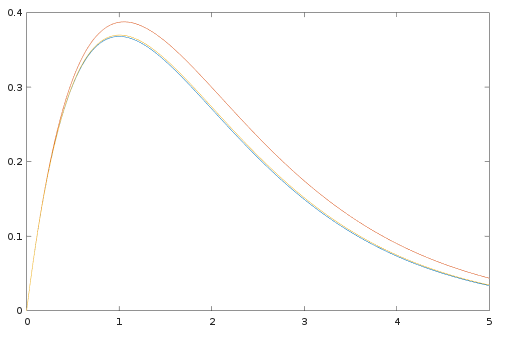
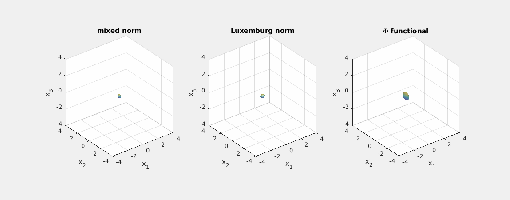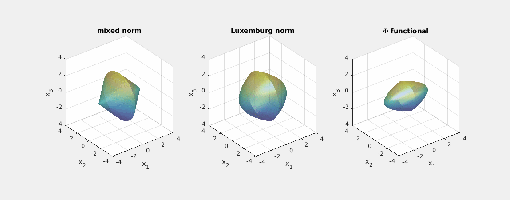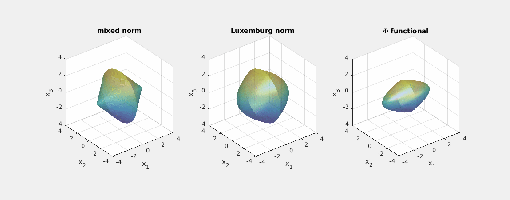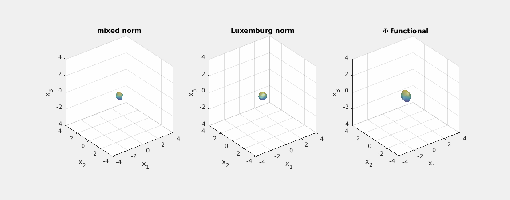
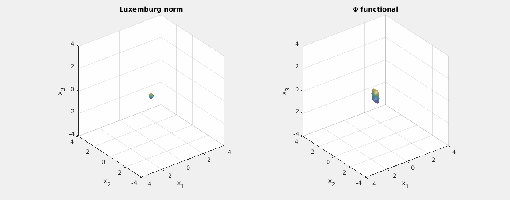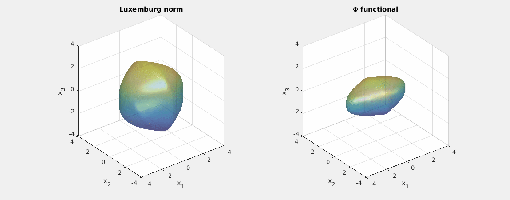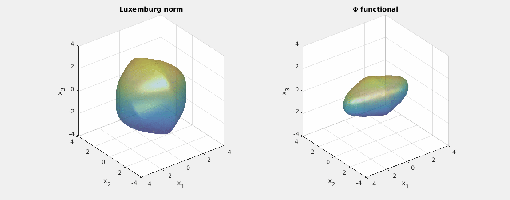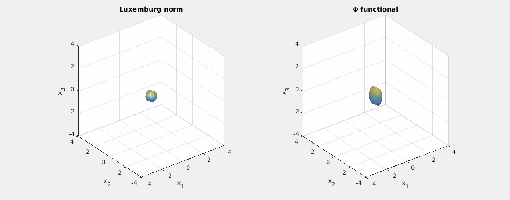
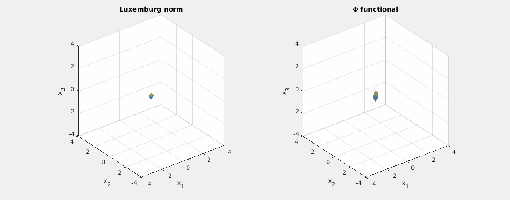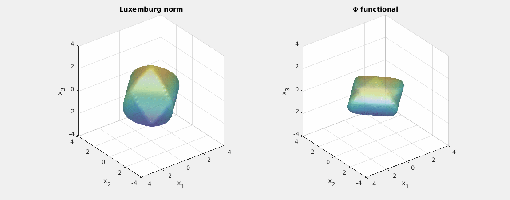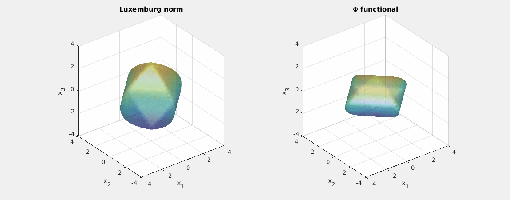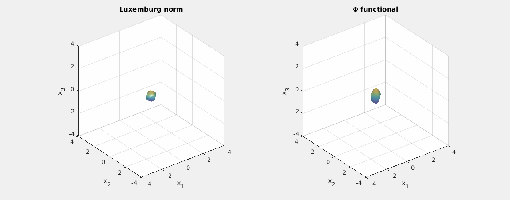Again note how the Luxemburg ball keeps its shape while the level sets of the 
, 
and 
. The mixed norm is again the 
. This implies that 
and thus, all 
.
and 
, then 
if and only if 
. 
we have 
and for 
we have 
. 
is a norm on 
we easily see that 
(since 
but since 
this can only hold if 
. For positive homogeneity observe
(which implies that 
and 
). Then it follows
as desired. 
lead to 
.
.
(which is not a norm):
]
regularize 