Mixing norms the Luxemburg way

In my last blog post I wrote about Luxemburg norms which are constructions to get norms out of a non-homogeneous function ${\phi:[0,\infty[\rightarrow[0,\infty[}$ which satisfies ${\phi(0) = 0}$ and are increasing and convex (and thus, continuous). The definition of the Luxemburg norm in this case is

$\displaystyle \|x\|_{\phi} := \inf\left\{\lambda>0\ :\ \sum_{k}\phi\left(\frac{|x_{k}|}{\lambda}\right)\leq 1\right\},$

and we saw that ${\|x\|_{\phi} = c}$ if ${\sum_{k}\phi\left(\frac{|x_{k}|}{c}\right)= 1}$ .

Actually, one can have a little more flexibility in the construction as one can also use different functions ${\phi}$ in each coordinate: If ${\phi_{k}}$ are functions as ${\phi}$ above, we can define

$\displaystyle \|x\|_{\phi_{k}} := \inf\left\{\lambda>0\ :\ \sum_{k}\phi_{k}\left(\frac{|x_{k}|}{\lambda}\right)\leq 1\right\},$

and it still holds that ${\|x\|_{\phi_{k}} = c}$ if and only if ${\sum_{k}\phi_{k}\left(\frac{|x_{k}|}{c}\right)= 1}$ . The proof that this construction indeed gives a norm is the same as in the one in the previous post.

This construction allows, among other things, to construct norms that behave like different ${p}$ -norms in different directions. Here is a simple example: In the case of ${x\in{\mathbb R}^{d}}$ we can split the variables into two groups, say the first ${k}$ variables and the last ${d-k}$ variables. The first group shall be treated with a ${p}$ -norm and the second group with a ${q}$ -norm. For the respective Luxemburg norm one has

$\displaystyle \|x\|:= \inf\left\{\lambda>0\ :\ \sum_{i=1}^{k}\frac{|x_{i}|^{p}}{\lambda^{p}} + \sum_{i=k+1}^{d}\frac{|x_{i}|^{q}}{\lambda^{q}}\leq 1\right\},$

Note that there is a different way to do a similar thing, namely a mixed norm defined as

$\displaystyle \|x\|_{p,q}:= \left(\sum_{i=1}^{k}|x_{i}|^{p}\right)^{1/p} + \left(\sum_{i=k+1}^{d}|x_{i}|^{q}\right)^{1/q}.$

As any two norms, these are equivalent, but they induce a different geometry. On top of that, one could in principle also consider ${\Phi}$ functionals

$\displaystyle \Phi_{p,q}(x) = \sum_{i=1}^{k}|x_{i}|^{p} + \sum_{i=k+1}^{d}|x_{i}|^{q},$

which is again something different.

A bit more general, we may consider all these three conditions for general partitions of the index sets and a different exponent for each set.

Here are some observations on the differences:

For the Luxemburg norm the only thing that counts are the exponents (or functions ${\phi_{k}}$ ). If you partition the index set into two parts but give the same exponents to both, the Luxemburg norm is the same as if you would consider the two parts as just one part.
The mixed norm is not the ${p}$ -norm, even if the set the exponent to ${p}$ for every part.
The Luxemburg norm has the flexibility to use other functionals than just the powers.
For the mixed norms one could consider additional mixing by not just summing the norms of the different parts, which is the same as taking the ${1}$ -norm of the vector of norms. Of course, other norms are possible, e.g. constructions like
$\displaystyle \left(\left(\sum_{i=1}^{k}|x_{i}|^{p}\right)^{r/p} + \left(\sum_{i=k+1}^{d}|x_{i}|^{q}\right)^{r/q}\right)^{1/r}$

are also norms. (Actually, the term mixed norm is often used for the above construction with ${p=q\neq r}$ .)

Here are some pictures that show the different geometry that these three functionals induce. We consider ${d=3}$ i.e., three-dimensional space, and picture the norm-balls (of level sets in the case the functionals ${\Phi}$ ).

Consider the case ${k=1}$ and the first exponent to be ${p=1}$ and the second ${q=2}$ . The mixed norm is
$\displaystyle \|x\|_{1,2} = |x_{1}| + \sqrt{x_{2}^{2}+x_{3}^{2}},$

the ${\Phi}$ -functional is

$\displaystyle \Phi(x)_{1,2} = |x_{1}| + x_{2}^{2}+x_{3}^{2},$

and for the Luxemburg norm it holds that

$\displaystyle \|x\| = c\iff \frac{|x_{1}|}{c} + \frac{x_{2}^{2} + x_{3}^{2}}{c^{2}} = 1.$

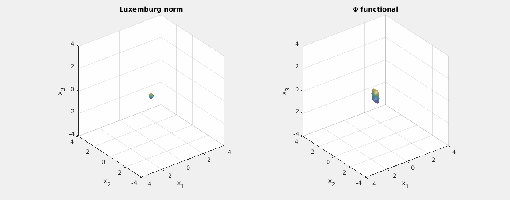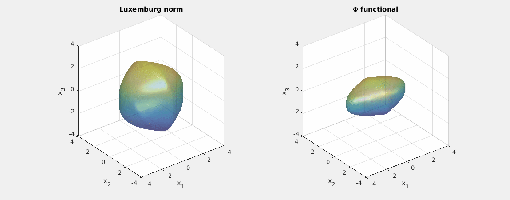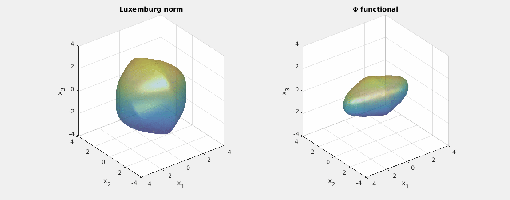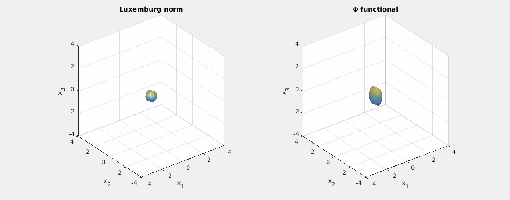
Here are animated images of the respective level sets/norm balls for radii ${0.25, 0.5, 0.75,\dots,3}$ :

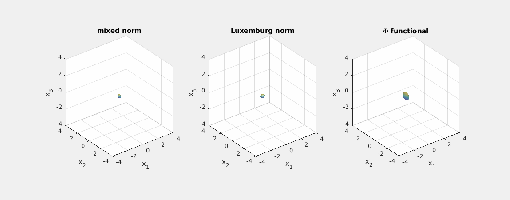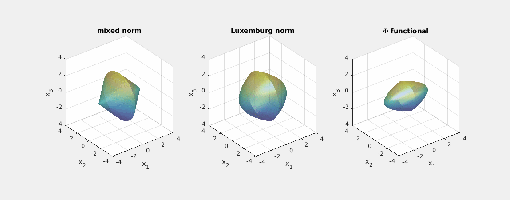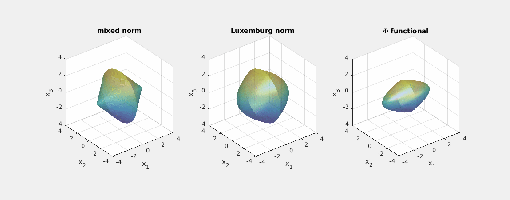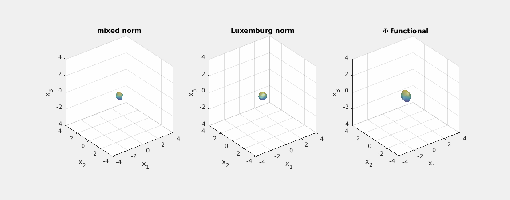
You may note the different shapes of the balls of the mixed norm and the Luxemburg norm. Also, the shape of their norm balls stays the same as you scale the radius. The last observation is not true for the ${\Phi}$ functional: Different directions scale differently.
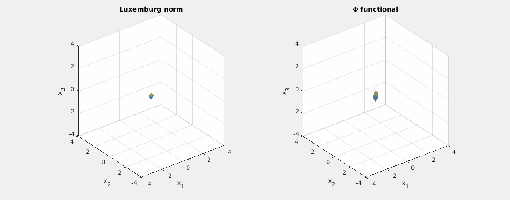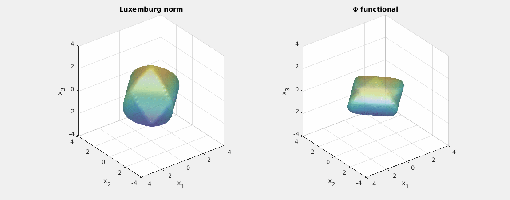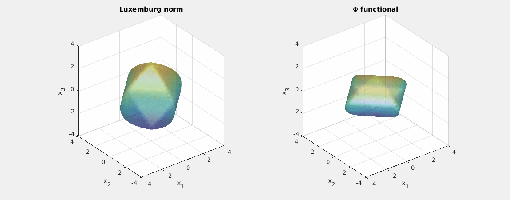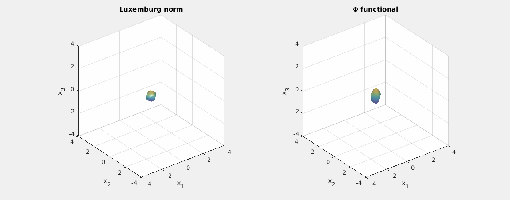
Now consider ${k=2}$ and the same exponents. This makes the mixed norm equal to the ${1}$ -norm, since
$\displaystyle \|x\|_{1,2} = |x_{1}| + |x_{2}| + \sqrt{x_{3}^{2}} = \|x\|_{1}.$

The ${\Phi}$ -functional is

$\displaystyle \Phi(x)_{1,2} = |x_{1}| + |x_{2}|+x_{3}^{2},$

and for the Luxemburg norm it holds that

$\displaystyle \|x\| = c\iff \frac{|x_{1}| + |x_{2}|}{c} + \frac{x_{3}^{2}}{c^{2}} = 1.$

Here are animated images of the respective level sets/norm balls of the ${\Phi}$ functional and the Luxemburg norm for the same radii as above (I do not show the balls for the mixed norm – they are just the standard cross-polytopes/ ${1}$ -norm balls/octahedra): Again note how the Luxemburg ball keeps its shape while the level sets of the ${\Phi}$ -functional changes shape while scaling.
Now we consider three different exponents: ${p_{1}=1}$ , ${p_{2} = 2}$ and ${p_{3} = 3}$ . The mixed norm is again the ${1}$ -norm. The ${\Phi}$ -functional is
$\displaystyle \Phi(x)_{1,2} = |x_{1}| + x_{2}^{2}+|x_{3}|^{3},$

and for the Luxemburg norm it holds that

$\displaystyle \|x\| = c\iff \frac{|x_{1}|}{c} + \frac{x_{2}^{2}}{c^{2}} + \frac{|x_{3}|^{3}}{c^{3}} = 1.$

Here are animated images of the respective level sets/norm balls of the ${\Phi}$ functional and the Luxemburg norm for the same radii as above (again, the balls for the mixed norm are just the standard cross-polytopes/ ${1}$ -norm balls/octahedra):