Building norms from increasing and convex functions: The Luxemburg norm

A function ${\phi:[0,\infty[\rightarrow[0,\infty[}$ is called ${p}$ -homogeneous, if for any ${t>0}$ it holds that ${\phi(tx) = t^{p}\phi(x)}$ . This implies that ${\phi(x) = x^{p}\phi(1)}$ and thus, all ${p}$ -homogeneous functions on the positive reals are just multiples of powers of ${p}$ . If you have such a power of ${p}$ you can form the ${p}$ -norm

$\displaystyle \|x\|_{p} = \left(\sum_{k}|x_{k}|^{p}\right)^{1/p}.$

By Minkowski’s inequality, this in indeed a norm for ${p\geq 1}$ .

If we have just some function ${\phi:[0,\infty[\rightarrow[0,\infty[}$ that is not homogeneous, we could still try to do a similar thing and consider

$\displaystyle \phi^{-1}\left(\sum_{k}\phi(|x_{k}|)\right).$

It is easy to see that one needs ${\phi(0)=0}$ and ${\phi}$ increasing and invertible to have any chance that this expression can be a norm. However, one usually does not get positive homogeneity of the expression, i.e. in general

$\displaystyle \phi^{-1}\left(\sum_{k}\phi(t|x_{k}|)\right)\neq t \phi^{-1}\left(\sum_{k}\phi(|x_{k}|)\right).$

A construction that helps in this situation is the Luxemburg-norm. The definition is as follows:

Definition 1 (and lemma). Let ${\phi:[0,\infty[\rightarrow[0,\infty[}$ fulfill ${\phi(0)=0}$ , ${\phi}$ be increasing and convex. Then we define the Luxemburg norm for ${\phi}$ as

$\displaystyle \|x\|_{\phi} := \inf\{\lambda>0\ :\ \sum_{k}\phi\left(\frac{|x_{k}|}{\lambda}\right)\leq 1\}.$

Let’s check if this really is a norm. To do so we make the following observation:

Lemma 2 If ${x\neq 0}$ , then ${c = \|x\|_{\phi}}$ if and only if ${\sum_{k}\phi\left(\frac{|x_{k}|}{c}\right) = 1}$ .

Proof: Basically follows by continuity of ${\phi}$ from the fact that for ${\lambda >c}$ we have ${\sum_{k}\phi\left(\frac{|x_{k}|}{\lambda}\right) \leq 1}$ and for ${\lambda<c}$ we have ${\sum_{k}\phi\left(\frac{|x_{k}|}{\lambda}\right) > 1}$ . $\Box$

Lemma 3 ${\|x\|_{\phi}}$ is a norm on ${{\mathbb R}^{d}}$ .

Proof: For ${x=0}$ we easily see that ${\|x\|_{\phi}=0}$ (since ${\phi(0)=0}$ ). Conversely, if ${\|x\|_{\phi}=0}$ , then ${\limsup_{\lambda\rightarrow 0}\sum_{k}\phi\left(\tfrac{|x_{k}|}{\lambda}\right) \leq 1}$ but since ${\lim_{t\rightarrow\infty}\phi(t) = \infty}$ this can only hold if ${x_{1}=\cdots=x_{d}= 0}$ . For positive homogeneity observe

$\displaystyle \begin{array}{rcl} \|tx\|_{\phi} & = & \inf\{\lambda>0\ :\ \sum_{k}\phi\left(\frac{|tx_{k}|}{\lambda}\right)\leq 1\}\\ & = & \inf\{|t|\mu>0\ :\ \sum_{k}\phi\left(\frac{|x_{k}|}{\mu}\right)\leq 1\}\\ & = & |t|\|x\|_{\phi}. \end{array}$

For the triangle inequality let ${c = \|x\|_{\phi}}$ and ${d = \|y\|_{\phi}}$ (which implies that ${\sum_{k}\phi\left(\tfrac{|x_{k}|}{c}\right)\leq 1}$ and ${\sum_{k}\phi\left(\tfrac{|y_{k}|}{d}\right)\leq 1}$ ). Then it follows

$\displaystyle \begin{array}{rcl} \sum_{k}\phi\left(\tfrac{|x_{k}+y_{k}|}{c+d}\right) &\leq& \sum_{k}\phi\left(\tfrac{c}{c+d}\tfrac{|x_{k}|}{c} +\tfrac{d}{c+d}\tfrac{|y_{k}|}{d}\right)\\ &\leq& \tfrac{c}{c+d}\underbrace{\sum_{k} \phi\left(\tfrac{|x_{k}|}{c}\right)}_{\leq 1} + \tfrac{d}{c+d}\underbrace{\sum_{k}\phi\left(\tfrac{|y_{k}|}{d}\right)}_{\leq 1}\\ &\leq& 1 \end{array}$

and this implies that ${c+d \geq \|x+y\|_{\phi}}$ as desired. $\Box$

As a simple exercise you can convince yourself that ${\phi(t) = t^{p}}$ lead to ${\|x\|_{\phi} = \|x\|_{p}}$ .

Let us see how the Luxemburg norm looks for other functions.

Example 1 Let ‘s take ${\phi(t) = \exp(t)-1}$ .

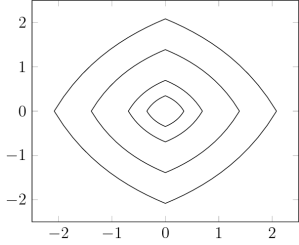
The function ${\phi}$ fulfills the conditions we need and here are the level lines of the functional ${x\mapsto \phi^{-1}\left(\sum_{k}\phi(|x_{k}|)\right)}$ (which is not a norm):

[Levels are ${0.5, 1, 2, 3}$ ]

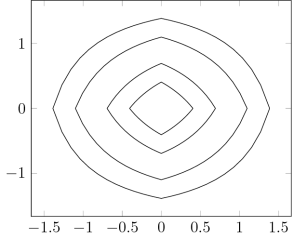
The picture shows that this functional is not a norm ad the shape of the “norm-balls” changes with the size. In contrast to that, the level lines of the respective Luxemburg norm look like this:

[Levels are ${0.5, 1, 2, 3}$ ]