How many samples are needed to reconstruct a sparse signal?
Well, there are many, many results around some of which you probably know (at least if you are following this blog or this one). Today I write about a neat result which I found quite some time ago on reconstruction of nonnegative sparse signals from a semi-continuous perspective.
1. From discrete sparse reconstruction/compressed sensing to semi-continuous
The basic sparse reconstruction problem asks the following: Say we have a vector  which only has
which only has 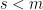 non-zero entries and a fat matrix
non-zero entries and a fat matrix  (i.e.
(i.e. 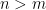 ) and consider that we are given measurements
) and consider that we are given measurements  . Of course, the system
. Of course, the system 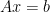 is underdetermined. However, we may add a little more prior knowledge on the solution and ask: Is is possible to reconstruct
is underdetermined. However, we may add a little more prior knowledge on the solution and ask: Is is possible to reconstruct  from
from  if we know that the vector
if we know that the vector  is sparse? If yes: How? Under what conditions on
is sparse? If yes: How? Under what conditions on 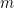 ,
,  ,
,  and
and  ? This question created the expanding universe of compressed sensing recently (and this universe is expanding so fast that for sure there has to be some dark energy in it). As a matter of fact, a powerful method to obtain sparse solutions to underdetermined systems is
? This question created the expanding universe of compressed sensing recently (and this universe is expanding so fast that for sure there has to be some dark energy in it). As a matter of fact, a powerful method to obtain sparse solutions to underdetermined systems is  -minimization a.k.a. Basis Pursuit on which I blogged recently: Solve
-minimization a.k.a. Basis Pursuit on which I blogged recently: Solve

and the important ingredient here is the  -norm of the vector in the objective function.
-norm of the vector in the objective function.
In this post I’ll formulate semi-continuous sparse reconstruction. We move from an 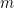 -vector
-vector  to a finite signed measure
to a finite signed measure  on a closed interval (which we assume to be
on a closed interval (which we assume to be ![{I=[-1,1]}](https://s0.wp.com/latex.php?latex=%7BI%3D%5B-1%2C1%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) for simplicty). We may embed the
for simplicty). We may embed the 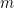 -vectors into the space of finite signed measures by choosing
-vectors into the space of finite signed measures by choosing 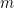 points
points 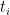 ,
, 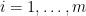 from the interval
from the interval 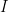 and build
and build 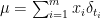 with the point-masses (or Dirac measures)
with the point-masses (or Dirac measures) 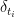 . To a be a bit more precise, we speak about the space
. To a be a bit more precise, we speak about the space  of Radon measures on
of Radon measures on 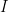 , which are defined on the Borel
, which are defined on the Borel  -algebra of
-algebra of 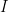 and are finite. Radon measures are not very scary objects and an intuitive way to think of them is to use Riesz representation: Every Radon measure arises as a continuous linear functional on a space of continuous functions, namely the space
and are finite. Radon measures are not very scary objects and an intuitive way to think of them is to use Riesz representation: Every Radon measure arises as a continuous linear functional on a space of continuous functions, namely the space 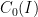 which is the closure of the continuous functions with compact support in
which is the closure of the continuous functions with compact support in ![{{]{-1,1}[}}](https://s0.wp.com/latex.php?latex=%7B%7B%5D%7B-1%2C1%7D%5B%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) with respect to the supremum norm. Hence, Radon measures work on these functions as
with respect to the supremum norm. Hence, Radon measures work on these functions as  . It is also natural to speak of the support
. It is also natural to speak of the support  of a Radon measure
of a Radon measure  and it holds for any continuous function
and it holds for any continuous function  that
that

An important tool for Radon measures is the Hahn-Jordan decomposition which decomposes  into a positive part
into a positive part  and a negative part
and a negative part  , i.e.
, i.e.  and
and  are non-negative and
are non-negative and  . Finally the variation of a measure, which is
. Finally the variation of a measure, which is

provides a norm on the space of Radon measures.
Example 1 For the measure 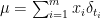 one readily calculates that
one readily calculates that
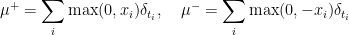
and hence
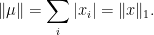
In this sense, the space of Radon measures provides a generalization of  .
.
We may sample a Radon measure  with
with  linear functionals and these can be encoded by
linear functionals and these can be encoded by  continuous functions
continuous functions 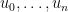 as
as

This sampling gives a bounded linear operator  . The generalization of Basis Pursuit is then given by
. The generalization of Basis Pursuit is then given by
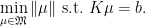
This was introduced and called “Support Pursuit” in the preprint Exact Reconstruction using Support Pursuit by Yohann de Castro and Frabrice Gamboa.
More on the motivation and the use of Radon measures for sparsity can be found in Inverse problems in spaces of measures by Kristian Bredies and Hanna Pikkarainen.
2. Exact reconstruction of sparse nonnegative Radon measures
Before I talk about the results we may count the degrees of freedom a sparse Radon measure has: If 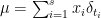 with some
with some  than
than  is defined by the
is defined by the  weights
weights  and the
and the  positions
positions 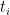 . Hence, we expect that at least
. Hence, we expect that at least 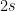 linear measurements should be necessary to reconstruct
linear measurements should be necessary to reconstruct  . Surprisingly, this is almost enough if we know that the measure is nonnegative! We only need one more measurement, that is
. Surprisingly, this is almost enough if we know that the measure is nonnegative! We only need one more measurement, that is  and moreover, we can take fairly simple measurements, namely the monomials:
and moreover, we can take fairly simple measurements, namely the monomials: 
 (with the convention that
(with the convention that 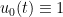 ). This is shown in the following theorem by de Castro and Gamboa.
). This is shown in the following theorem by de Castro and Gamboa.
Theorem 1 Let 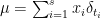 with
with 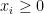 ,
, 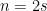 and let
and let  ,
, 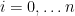 be the monomials as above. Define
be the monomials as above. Define 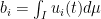 . Then
. Then  is the unique solution of the support pursuit problem, that is of
is the unique solution of the support pursuit problem, that is of
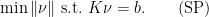
Proof: The following polynomial will be of importance: For a constant 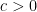 define
define
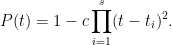
The following properties of 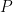 will be used:
will be used:
-
 for
for 
-
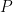 has degree
has degree 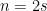 and hence, is a linear combination of the
and hence, is a linear combination of the  ,
, 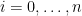 , i.e.
, i.e. 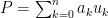 .
.
- For
 small enough it holds for
small enough it holds for 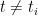 that
that  .
.
Now let  be a solution of (SP). We have to show that
be a solution of (SP). We have to show that 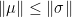 . Due to property 2 we know that
. Due to property 2 we know that

Due to property 1 and non-negativity of  we conclude that
we conclude that
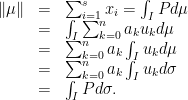
Moreover, by Lebesgue’s decomposition we can decompose  with respect to
with respect to  such that
such that
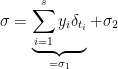
and 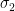 is singular with respect to
is singular with respect to  . We get
. We get
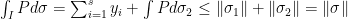
and we conclude that 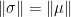 and especially
and especially 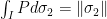 . This shows that
. This shows that  is a solution to
is a solution to  . It remains to show uniqueness. We show the following: If there is a
. It remains to show uniqueness. We show the following: If there is a  with support in
with support in 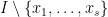 such that
such that 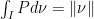 , then
, then 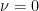 . To see this, we build, for any
. To see this, we build, for any 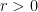 , the sets
, the sets
![\displaystyle \Omega_r = [-1,1]\setminus \bigcup_{i=1}^s ]x_i-r,x_i+r[.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5COmega_r+%3D+%5B-1%2C1%5D%5Csetminus+%5Cbigcup_%7Bi%3D1%7D%5Es+%5Dx_i-r%2Cx_i%2Br%5B.+&bg=ffffff&fg=000000&s=0&c=20201002)
and assume that there exists 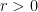 such that
such that 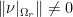 (
( denoting the restriction of
denoting the restriction of  to
to  ). However, it holds by property 3 of
). However, it holds by property 3 of 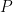 that
that

and consequently
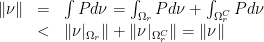
which is a contradiction. Hence,  for all
for all  and this implies
and this implies 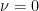 . Since
. Since 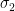 has its support in
has its support in 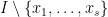 we conclude that
we conclude that 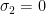 . Hence the support of
. Hence the support of  is exactly
is exactly 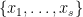 . and since
. and since  and hence
and hence  . This can be written as a Vandermonde system
. This can be written as a Vandermonde system

which only has the zero solution, giving 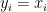 .
. 
3. Generalization to other measurements
The measurement by monomials may sound a bit unusual. However, de Castro and Gamboa show more. What really matters here is that the monomials for a so-called Chebyshev-System (or Tchebyscheff-system or T-system – by the way, have you ever tried to google for a T-system?). This is explained, for example in the book “Tchebycheff Systems: With Applications in Analysis and Statistics” by Karlin and Studden. A T-system on 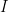 is simply a set of
is simply a set of  functions
functions 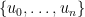 such that any linear combination of these functions has at most
such that any linear combination of these functions has at most  zeros. These systems are called after Tchebyscheff since they obey many of the helpful properties of the Tchebyscheff-polynomials.
zeros. These systems are called after Tchebyscheff since they obey many of the helpful properties of the Tchebyscheff-polynomials.
What is helpful in our context is the following theorem of Krein:
Theorem 2 (Krein) If 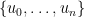 is a T-system for
is a T-system for 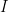 ,
, 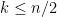 and
and  are in the interior of
are in the interior of 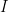 , then there exists a linear combination
, then there exists a linear combination 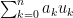 which is non-negative and vanishes exactly the the point
which is non-negative and vanishes exactly the the point 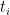 .
.
Now consider that we replace the monomials in Theorem~1 by a T-system. You recognize that Krein’s Theorem allows to construct a “generalized polynomial” which fulfills the same requirements than the polynomial 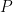 is the proof of Theorem~1 as soon as the constant function 1 lies in the span of the T-system and indeed the result of Theorem~1 is also valid in that case.
is the proof of Theorem~1 as soon as the constant function 1 lies in the span of the T-system and indeed the result of Theorem~1 is also valid in that case.
4. Exact reconstruction of  -sparse nonnegative vectors from
-sparse nonnegative vectors from  measurements
measurements
From the above one can deduce a reconstruction result for  -sparse vectors and I quote Theorem 2.4 from Exact Reconstruction using Support Pursuit:
-sparse vectors and I quote Theorem 2.4 from Exact Reconstruction using Support Pursuit:
Theorem 3 Let  ,
, 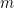 ,
,  be integers such that
be integers such that 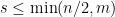 and let
and let 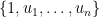 be a complete T-system on
be a complete T-system on 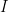 (that is,
(that is, 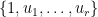 is a T-system on
is a T-system on 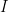 for all
for all 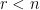 ). Then it holds: For any distinct reals
). Then it holds: For any distinct reals 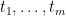 and
and  defined as
defined as

Basis Pursuit recovers all nonnegative  -sparse vectors
-sparse vectors  .
.
5. Concluding remarks
Note that Theorem~3 gives a deterministic construction of a measurement matrix.
Also note, that nonnegativity is crucial in what we did here. This allowed (in the monomial case) to work with squares and obtain the polynomial 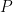 in the proof of Theorem~1 (which is also called “dual certificate” in this context). This raises the question how this method can be adapted to all sparse signals. One needs (in the monomial case) a polynomial which is bounded by 1 but matches the signs of the measure on its support. While this can be done (I think) for polynomials it seems difficult to obtain a generalization of Krein’s Theorem to this case…
in the proof of Theorem~1 (which is also called “dual certificate” in this context). This raises the question how this method can be adapted to all sparse signals. One needs (in the monomial case) a polynomial which is bounded by 1 but matches the signs of the measure on its support. While this can be done (I think) for polynomials it seems difficult to obtain a generalization of Krein’s Theorem to this case…
be a compact subset of
and consider the space
of continuous functions
with the usual supremum norm. The Riesz Representation Theorem states that the dual space of
is in this case the set of all Radon measures, denoted by
and the canonical duality pairing is given by
with the usual notion of weak* convergence which read as
positive if
implies that
. If a positive measure satisfies
(i.e. it integrates the constant function with unit value to one), we call it a probability measure and we denote with
the set of all probability measures.
with
induces a probability measure via
-measures: For every
there is the
-measure at this point, defined by
of probability measure is the generalization of the standard simplex in
to infinite dimensions (in fact uncountably many dimensions): The
-measures are the extreme points of
and since the set
is compact in the weak* topology, the Krein-Milman Theorem states that
is the weak*-closure of the set of convex combinations of the
-measures – similarly as the standard simplex in
is the convex combination of the canonical basis vectors of
.
is the set of convex combinations of the measures
(
). Hence,
resembles the hyper-octahedron (aka cross polytope or
-ball).
,
and suppose that the subset
of
consisting of the probability measures
such that for
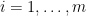
such that
and
are convex combinations of at most
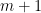
-measures, and
we have
measured by
linear measurements, there are two extremal ones which consists of
-measures.
does not make much sense, since
for all
.