Let {\Omega} be a compact subset of {{\mathbb R}^d} and consider the space {C(\Omega)} of continuous functions {f:\Omega\rightarrow {\mathbb R}} with the usual supremum norm. The Riesz Representation Theorem states that the dual space of {C(\Omega)} is in this case the set of all Radon measures, denoted by {\mathfrak{M}(\Omega)} and the canonical duality pairing is given by

\displaystyle \langle\mu,f\rangle = \mu(f) = \int_\Omega fd\mu.

We can equip {\mathfrak{M}(\Omega)} with the usual notion of weak* convergence which read as

\displaystyle \mu_n\rightharpoonup^* \mu\ \iff\ \text{for every}\ f:\ \mu_n(f)\rightarrow\mu(f).

We call a measure {\mu} positive if {f\geq 0} implies that {\mu(f)\geq 0}. If a positive measure satisfies {\mu(1)=1} (i.e. it integrates the constant function with unit value to one), we call it a probability measure and we denote with {\Delta\subset \mathfrak{M}(\Omega)} the set of all probability measures.

Example 1 Every non-negative integrable function {\phi:\Omega\rightarrow{\mathbb R}} with {\int_\Omega \phi(x)dx} induces a probability measure via

\displaystyle f\mapsto \int_\Omega f(x)\phi(x)dx.

Quite different probability measures are the {\delta}-measures: For every {x\in\Omega} there is the {\delta}-measure at this point, defined by

\displaystyle \delta_x(f) = f(x).

In some sense, the set {\Delta} of probability measure is the generalization of the standard simplex in {{\mathbb R}^n} to infinite dimensions (in fact uncountably many dimensions): The {\delta}-measures are the extreme points of {\Delta} and since the set {\Delta} is compact in the weak* topology, the Krein-Milman Theorem states that {\Delta} is the weak*-closure of the set of convex combinations of the {\delta}-measures – similarly as the standard simplex in {{\mathbb R}^n} is the convex combination of the canonical basis vectors of {{\mathbb R}^n}.

Remark 1 If we drop the positivity assumption and form the set

\displaystyle O = \{\mu\in\mathfrak{M}(\Omega)\ :\ |f|\leq 1\implies |\mu(f)|\leq 1\}

we have the {O} is the set of convex combinations of the measures {\pm\delta_x} ({x\in\Omega}). Hence, {O} resembles the hyper-octahedron (aka cross polytope or {\ell^1}-ball).

I’ve taken the above (with almost similar notation) from the book “ A Course in Convexity” by Alexander Barvinok. I was curious to find (in Chapter III, Section 9) something which reads as a nice glimpse on semi-continuous compressed sensing: Proposition 9.4 reads as follows

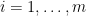
Proposition 1 Let {g,f_1,\dots,f_m\in C(\Omega)}, {b\in{\mathbb R}^m} and suppose that the subset {B} of {\Delta} consisting of the probability measures {\mu} such that for {i=1,\dots,m}

\displaystyle \int f_id\mu = b_i

is not empty. Then there exists {\mu^+,\mu^-\in B} such that

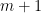
  1. {\mu^+} and {\mu^-} are convex combinations of at most {m+1} {\delta}-measures, and
  2. it holds that for all {\mu\in B} we have

    \displaystyle \mu^-(g)\leq \mu(g)\leq \mu^+(g).

In terms of compressed sensing this says: Among all probability measures which comply with the data {b} measured by {m} linear measurements, there are two extremal ones which consists of {m+1} {\delta}-measures.

Note that something similar to “support-pursuit” does not work here: The minimization problem {\min_{\mu\in B, \mu(f_i)=b_i}\|\mu\|_{\mathfrak{M}}} does not make much sense, since {\|\mu\|_{\mathfrak{M}}=1} for all {\mu\in B}.