Here is a lemma that I find myself googling regularly since I always forget it’s exact form.
Lemma 1 Let
be a monotone operator,
and denote by
the resolvent of
. Then it holds that
Proof: We start with the left hand side and deduce
I do not know any official name of this, but would call it Moreau’s identity which is the name of the respective statement for proximal operators for convex functions and
:
The version for monotone operators is Proposition 23.18 in the first edition of Bauschke and Combette’s book “Convex Analysis and Monotone Operator Theory in Hilbert Spaces”.
February 24, 2017 at 11:29 pm
Moreau’s identity can also be written as x = R_A(x) + R_Ainv (x) (assuming lambda is 1 for simplicity). This way of writing it emphasizes that Moreau’s identity is a generalization of the linear algebra fact that x = P_W (x) + P_Wperp (x), where W is a subspace of a finite dimensional inner product space and Wperp is the orthogonal complement of W.
February 25, 2017 at 12:39 am
That’s correct – I mainly wrote this down because I always forget the scaling in the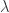 . Unfortunately this does not suggest itself from the projection formulation…
. Unfortunately this does not suggest itself from the projection formulation…
March 1, 2017 at 6:50 pm
Does this also hold for general operators A? I didn’t see where you used the monotonicity …
March 1, 2017 at 8:56 pm
That’s true, you only need that the resolvents exist.
March 2, 2017 at 8:37 pm
Dirk, you must remove the parentheses around (I – λ prox) … or next time you code a primal-dual algorithm, you’ll get headache.
March 2, 2017 at 10:36 pm
Oh yeah, thanks!